7. Apresentar e discutir a relação estabelecida entre a sequência de Fibonacci e a noção de proporção áurea.
A proporção áurea ou número de ouro, é uma constante real algébrica irracional em formato de dizima, ou apenas, um número que simplesmente é encontrado na forma de diferentes coisas no nosso mundo, como os filamentos de folha, girassóis, conchas de caracóis, furacões, ondas no mar e até nas proporções do corpo humano.
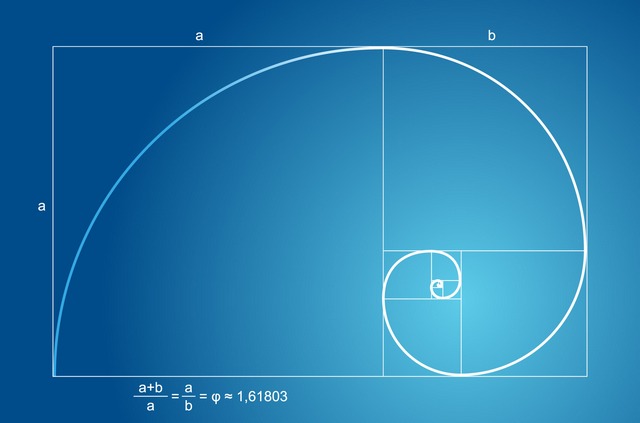
Uma forma gráfica de obter a proporção é partir de um quadrado, dividindo-o em duas partes, dessa vez iguais, usando uma reta vertical central e usar a parte direita para conseguir uma diagonal que começa no canto inferior esquerdo e termina no superior direito dessa mesma parte, gira-se esta diagonal até a base da figura e constrói-se um retângulo áureo a partir dessa nova largura.
Leonardo de Pisa ou Fibonacci foi o primeiro grande matemático europeu da Idade Média e durante seus estudos, descobriu propriedades únicas de uma sequência específica de números, que mais tarde seria nomeada como Sequência de Fibonacci. A sequência de números começa como os números decimais, com 0 e 1 e os próximos números são dados de acordo com a soma dos dois anteriores, então temos isso:
0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
A ligação com a proporção áurea é quando lidamos com a razão entre um número qualquer e seu antecessor, percebemos que quanto mais a sequência progride, mais a razão dentre estes números se aproxima do número de ouro:
2/1 = 2 | 3/2 = 1,5 | 5/3 = 1,6 | 8/5 = 1,6 | 13/8 = 1,625 | 21/13 = 1,615 | 34/21 = 1,619 | 55/34 = 1,617 | 89/55 = 1,6181 …
O retângulo de ouro, mostrado anteriormente, é executado a partir da sequência de Fibonacci, por isso seus estudos foram tão importantes.
A proporção áurea é relacionada ao que é belo pelo cérebro humano, não se sabe ainda o motivo exato desta ocorrência, mas o retângulo perfeito ou o caracol áureo são as formas do que o ser humano considera mais belo. Após as pessoas descobrirem isso, passaram a usa-la em suas criações. Por exemplo, a Monalisa de Leonardo Da Vinci.
Até hoje muitos designers usam essa proporção em seus trabalhos, cartazes de filmes, páginas da web, cenas de series e etc.
A proporção áurea ou número de ouro, é uma constante real algébrica irracional em formato de dizima, ou apenas, um número que simplesmente é encontrado na forma de diferentes coisas no nosso mundo, como os filamentos de folha, girassóis, conchas de caracóis, furacões, ondas no mar e até nas proporções do corpo humano.
Uma forma gráfica de obter a proporção é partir de um quadrado, dividindo-o em duas partes, dessa vez iguais, usando uma reta vertical central e usar a parte direita para conseguir uma diagonal que começa no canto inferior esquerdo e termina no superior direito dessa mesma parte, gira-se esta diagonal até a base da figura e constrói-se um retângulo áureo a partir dessa nova largura.
Leonardo de Pisa ou Fibonacci foi o primeiro grande matemático europeu da Idade Média e durante seus estudos, descobriu propriedades únicas de uma sequência específica de números, que mais tarde seria nomeada como Sequência de Fibonacci. A sequência de números começa como os números decimais, com 0 e 1 e os próximos números são dados de acordo com a soma dos dois anteriores, então temos isso:
0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
A ligação com a proporção áurea é quando lidamos com a razão entre um número qualquer e seu antecessor, percebemos que quanto mais a sequência progride, mais a razão dentre estes números se aproxima do número de ouro:
2/1 = 2 | 3/2 = 1,5 | 5/3 = 1,6 | 8/5 = 1,6 | 13/8 = 1,625 | 21/13 = 1,615 | 34/21 = 1,619 | 55/34 = 1,617 | 89/55 = 1,6181 …
O retângulo de ouro, mostrado anteriormente, é executado a partir da sequência de Fibonacci, por isso seus estudos foram tão importantes.
A proporção áurea é relacionada ao que é belo pelo cérebro humano, não se sabe ainda o motivo exato desta ocorrência, mas o retângulo perfeito ou o caracol áureo são as formas do que o ser humano considera mais belo. Após as pessoas descobrirem isso, passaram a usa-la em suas criações. Por exemplo, a Monalisa de Leonardo Da Vinci.
Até hoje muitos designers usam essa proporção em seus trabalhos, cartazes de filmes, páginas da web, cenas de series e etc.


Comentários
Postar um comentário